What is OSL dating?
Introduction
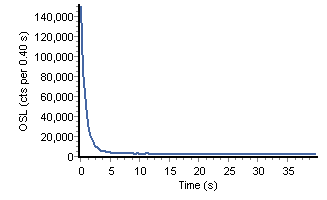
Fig. 1: Shinedown curve for quartz grains showing >95% reduction in OSL within 4 seconds of exposure to light from blue diodes
Optically stimulated luminescence (OSL) dating or optical dating provides a measure of time since sediment grains were deposited and shielded from further light or heat exposure, which often effectively resets the luminescence signal (Fig.1). This technique, as thermoluminescence, was originally developed in the 1950s and 1960s to date fired archaeological materials, like ceramics (Aitken, 1985). Ensuing research in the 1970s documented that marine and other sediments with a prior sunlight exposure of hours to days were suitable for thermoluminescence dating (Wintle and Huntley, 1980). Discoveries in the 1980s and 1990s that exposure of quartz and feldspar grains to a tunable light source, initially with lasers and later by light emitting diodes, yield luminescence components that are solar reset within seconds to minutes, expanded greatly the utility of the method (Huntley et al., 1985; Hütt et al., 1988; Aitken, 1998). In the past 15 years there have been significant advances in luminescence dating with the advent of single aliquot and grain analysis, and associated protocols with blue/green diodes that can effectively compensated for laboratory induced sensitivity changes (Murray and Wintle, 2003; Wintle and Murray, 2006; Duller, 2012) and render accurate ages for the past ca. 150,000 years. Most recently, the development of protocols for inducing the thermal-transfer of deeply trapped electrons has extended potentially OSL dating to the 106 year timescale for well solar-reset quartz and potassium feldspar grains from eolian and littoral environments (Duller and Wintle, 2012).
Common silicate minerals like quartz and potassium feldspar contain lattice-charge defects formed during crystallization and from subsequent exposure to ionizing radiation. These charge defects are potential sites of electron storage with a variety of trap-depth energies. A subpopulation of stored electrons with trap depths of ~1.3 to 3 eV is a subsequent source for time-diagnostic luminescence emissions. Free electrons are generated within the mineral matrix by exposure to ionizing radiation from the radioactive decay of daughter isotopes in the 235U, 238U and 232Th decay series, and a radioactive isotope of potassium, 40K, with lesser contributions from the decay of 85Rb and cosmic sources. The radioactive decay of 40K releases beta and gamma radiation, whereas the decay in the U and Th series generates mostly alpha particles and some beta and gamma radiation. Alpha particles are about 90 to 95% less effective in inducing luminescence compared to beta and gamma radiation. Thus, the population of stored electrons in lattice-charge defects increases with prolonged exposure to ionizing radiation and the resolved luminescence emission increases with time. Exposure of mineral grains to light or heat (at least 300˚C) reduces the luminescence to a low and definable residual level. Often this luminescence “cycle" occurs repeatedly in many depositional environments with signal acquisition of mineral grains by exposure to ionizing radiation during the burial period and signal resetting (“zeroing") with light exposure concurrent to sediment erosion and transportation. Often mineral grains that are fresh from a bedrock sources have significantly lower luminescence emissions per radiation dose in comparison to grains that have cycled repeatedly. OSL dating provides an estimate of the time elapsed with latest period of burial and thus, yields a depositional age (Fig. 1).
Principles of Luminescence Dating
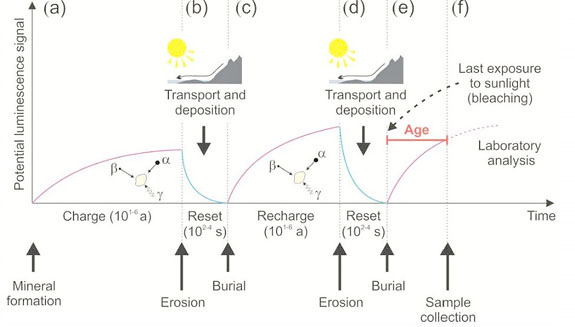
Fig. 2: Processes associated with OSL dating. (a) Luminescence is acquired in mineral grains with exposure to ionizing radiation and trapping of electrons. (b) The luminescence for grains is zeroed by exposure to sunlight with erosion and transport. (c) With burial and exposure to ionizing radiation free electrons are stored in charge defects within grains crystal lattice. (d) Further light exposure of grains with erosion and transport zeros the luminescence. (e) The grains are buried again and luminescence is acquired with exposure to ionizing radiation. (f) Careful sampling without light exposure and measuring of the natural luminescence, followed by a normalizing test dose (Ln/Tn) compared to the regenerative dose to yield an equivalent dose (De) (from Mellet, 2013).
The exposure of quartz and feldspar grains to sunlight for >60 seconds effectively diminishes the time-stored OSL signal to a low definable level. This residual level is the point from which the geological OSL signal accumulates post burial. Many types of sediment receive prolonged (> 1 hr) light exposure with transport and deposition, particularly in eolian, littoral and sublittoral sedimentary environments. In addition, the inherent residual level is influenced by the susceptibility of the luminescence signal of a specific mineral to solar resetting. The OSL signal of potassium feldspar is usually more resista nt to solar resetting than most quartz. There is significant variability in the luminescence properties of quartz and potassium feldspar grains related to crystalline structure, minor and rare-earth impurities, solid-solution relations, number of luminescence cycles (Fig. 1) and radiation history (Mejdahl 1986). Thus, because of this inherent variability in dose sensitivity of quartz and feldspar, analytical procedures for dating often need to be tailored for a specific geologic provenance. The advent of single aliquot regenerative (SAR) dose procedures for quartz (Murray and Wintle, 2003; Wintle and Murray, 2006) has provided the needed analytical flexibility to compensate for variable luminescence properties of quartz and feldspar grains and laboratory-induced sensitivity changes, particularly associated with preheat treatments and with laboratory beta irradiation.
OSL dating is predicated on measurements of a specific mineral and particle size, usually quartz or potassium feldspar. Mineral separations are performed by standard techniques using heavy liquids and hydrofluoric acid (HF) to digest non-quartz minerals and etch the outer 10 to 20 µm of quartz grains which are affected alpha radiation. The purity of the quartz extract is primal for effective dating because a small amount contamination (1%) by potassium feldspar and other minerals can dominate the luminescence emissions. Multiple soaks in HF may be needed to obtain a pure quartz separate. Purity of the separate is accessed through microscopic inspection and point counting of grain mineralogy. Spectral purity of quartz is often determined by excitation by infrared light from a diode array with subsequent light emissions associated presumably with feldspar contaminants. However, some quartz grains yield considerable emissions with infrared excitation and may host feldspathic or other mineral inclusions; such grains should be analyzed as feldspar grains.
Sediment grains act as long-term radiation dosimeters when shielded from further light exposure with the luminescence signal a measure of radiation exposure during the burial period. The radiation dose that is equivalent to the natural luminescence emission of isolated quartz and feldspar grains is referred to as the equivalent dose (De: measured in grays: 100 rads = 1 gray) and is one half of the OSL age equation (Eq. 1). In most dating applications quartz is often the favored mineral because of its abundance in sediments, ease of physical separation and known stability of luminescence emissions. In contrast, feldspar minerals are often less abundant, and have a troubling signal instability (anomalous fading), though yield considerably brighter OSL emissions. The recent development of charge transfer techniques for potassium feldspar (e.g. post IR290) that use elevated preheats (~290˚C) to transfer electrons from stable deeper to shallower traps for ease of measurement has extended dating possibilities to 105 to 106 timescales for well solar reset grains (Duller and Wintle, 2012). Similar protocols have been also developed for quartz that has been particularly useful for dating Pleistocene loess deposits (e.g. Brown and Forman, 2012).
Determining OSL ages by Single Aliquot or single grain Regeneration Procedures
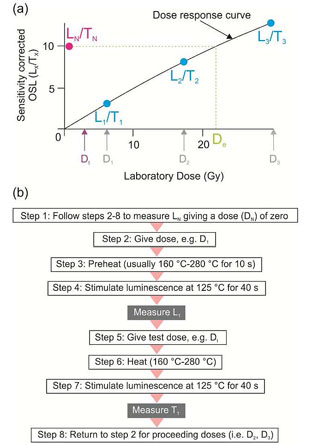
Fig. 3: (a) Determination of equivalent dose (in grays) using the single aliquot regenerative (SAR) protocols, where the natural luminescence emission is Ln/Tn and the regenerative dose is Lx/Tx; sensitivity changes are corrected by the administration of a small text dose (e.g. 5 grays). (b) Generalized SAR protocol (from Mellet, 2013).
A common approach in OSL dating is to use SAR protocols on quartz aliquots with the protocols customized for a specific sample, a study site or area (Fig. 3). The SAR approach is predicated on a number of assumptions. First, that the fast component of luminescence emissions, light released within the first 4 seconds, is the dominant signal, usually > 90% of the total light output above background levels. Second, the zero dose ratio is <5% of the natural ratio. Furthermore, the natural ratio is not at dose saturation that errors in calculating aliquot or grain equivalent doses are ≤10% and the recycling ratio is between 1.1 and 0.9; a measure of the coincident of the first and the last same regenerative dose and indicative that the test dose compensates well for sensitivity changes (Murray and Wintle, 2003). A critical practice in luminescence dating is the application of preheats (160 to 260˚C) to isolate a stable and a time-indicative luminescence emission (Fig. 2). The accuracy of the SAR protocols are evaluated by applying a known dose and testing for specific heat treatments within a sequence of analysis (Fig. 2) if the known dose can be recovered. Often such tests indicate that the known dose can be recovered using a variety of preheat treatments. In practice, using the SAR protocols to determine an equivalent dose involves calculation of a ratio between the natural luminescence and the luminescence from a known test dose (Ln/Tn ratio), which is compared to the luminescence emissions for regenerative doses (Lx/Tx) and also divided by the luminescence from the same test dose (Fig. 2). Applying a known test dose with each measurement cycle provides a metric to correct for changes in the sensitivity of the dated quartz grain(s) to acquire luminescence. Often with each successive measurement cycle the luminescence output increases by 5 to 15% or more from the same radiation dose.
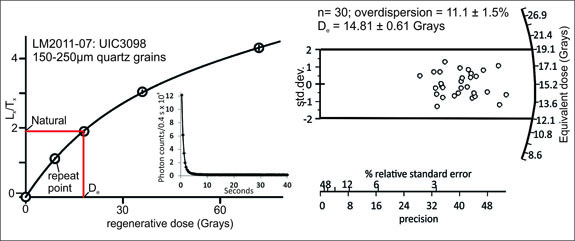
The equivalent dose using the SAR protocols are determined often on >30 aliquots of quartz or feldspar grains (Fig. 4). Each aliquot often contains 10’s to 100’s of quartz grains; the total number dependent on grain size (e.g. 100-150 µm), plate area and luminescence yield. Statistical analyses of equivalent dose distributions are critical to render accurate OSL ages with specific age models (Galbraith and Roberts, 2012). A common metric used is an overdispersion percentage of a De distribution and is an estimate of the relative standard deviation from a central De value in context of a statistical estimate of errors. A zero overdispersion percentage indicates high internal consistency in De values with 95% of the De values within 2σ errors, though rarely, if ever is a naught value calculated with equivalent dose data. Overdispersion values ~≤ 20% (at two sigma errors) are routinely assessed for quartz grains that are well solar reset, like eolian sands (e.g. Olley et al., 2004; Wright et al., 2011) and this value is considered a threshold metric for calculation of a De value using the central age model of Galbraith and Roberts (2012). Overdispersion values >20% may indicate mixing of grains of various ages or the partial solar resetting of grains, though overdispersion values up to 32% have been associated with a single equivalent dose population, particularly if the equivalent dose distribution is symmetrical (Arnolds and Roberts, 2009). The minimum or maximum age model may be an appropriate statistical treatment for equivalent dose data that is positively or negatively skewed (Galbraith and Roberts, 2012), depending on the pedologic and the sedimentologic context. The net effect of pedogenesis and bioturbation is often the mixing in of younger grains and thus a maximum age model may be appropriate (Ahr et al., 2013). In contrast, high energy fluvial and colluvial depositional environments often incorporate partially solar reset grains, thus the minimum age model may be appropriate. Other numeric treatments such as finite mixture modeling may also be applicable for separating multiple populations of equivalent dose (Galbraith and Green, 1999). The efficacy of these numeric analyses for isolating grain populations should be questioned and independent tests of accuracy are advised.
Fig. 4. Representative regenerative dose growth curves, with inset showing representative natural shine down curve, and radial plots of equivalent dose values on small aliquots (2-mm plate of 150-250 μm quartz fraction grains).
Another advantageous approach in OSL dating is single grain dating using the SAR protocols (e.g. Duller, 2008; 2012). Dating single grains of quartz and feldspar is particularly suitable with a mixture of grain populations in sediments, a common occurrence in some fluvial and colluvial sedimentary environments. A significant challenge with single grain dating is that often 1000’s of quartz grains need to be analyzed because 20 to 90% of the grains yield little or no luminescence emissions. Thus, a single age determination can occupy a luminescence reader for weeks to months to render sufficient number of analyses to statistically separate equivalent dose populations. Though this approach is time consuming, highly credible data is generated for identifying different equivalent dose grain populations and ultimately accurate ages.
Environmental Dose rate
A determination of the environmental dose rate (grays/ka) is a needed to render an OSL age (Eq. 1), which is an estimate of the exposure of mineral grains to ionizing radiation from the decay of U and Th series, 40K, and cosmic sources during the burial period. The U, Th and 40K content of the sediments can be determined by elemental analyses by neutron activation analyses or inductively coupled plasma-mass spectrometry; though such analyses assume secular equilibrium in the U and Th decay series. A suitable alternative is either gamma spectrometry in the field or in laboratory; the laboratory variant (Germanium gamma spectrometry) can detect isotopic disequilibrium in the U and Th decay series. If disequilibrium is detected the dose rate should be suitably modified. The beta and gamma doses should be adjusted according to grain diameter to compensate for mass attenuation (Fain et al., 1999). There is no appreciable alpha dose for coarse grains (> 50 µm) with the outer 10-20 µm of grains etched by soaking in HF during preparation. Fine grain sediments (< 40 µm) are fully affected by alpha radiation. A cosmic ray component must be included in dose rate calculations which compensates for geographic position, elevation, depth of burial and density of burial material (Prescott and Hutton, 1994). An estimate of the moisture content (by weight) during the burial period is also needed for age calculation. Often estimating moisture is difficult because there are few sedimentologic or diagetic criteria to quantify changes in moisture content during the burial period. Thus, realistic moisture contents are usually derived from particle size considerations, measured moisture contents in an undisturbed setting, evaluation of sediment compaction, level of water table to sampling site and climatic conditions; and appropriate uncertainty (10-20%) should be included.